XIX Olimpiada Nacional Escolar de Matemática (ONEM 2023) Etapa DRE - Nivel 2
9 de noviembre de 2023
Estimado estudiante, recibe por parte del equipo encargado de la organizaci´on las felicitaciones por estar participando en esta etapa de la Olimpiada Nacional Escolar de Matemática. Te recomendamos tener en consideración lo siguiente:
- Tienes un tiempo máximo de 2 horas para resolver estos retos matemáticos que te planteamos.
- Ten en cuenta que no está permitido el uso de calculadoras y otros recursos de consulta como apuntes o libros.
- Al momento que consideres que has culminado tu participación, haz entrega de la hoja de respuestas. En caso de ocurrir un empate se tomar´a en cuenta la hora de entrega.
- Queda bajo responsabilidad de los especialistas, docentes y estudiantes la no difusión de la prueba por ningún medio.
- Teniendo en cuenta estas indicaciones nos ayudar´as a que la olimpiada se realice de la mejor forma posible.
ESCRIBE EL RESULTADO DE CADA PROBLEMA EN LA HOJA DE RESPUESTAS. EN TODOS LOS CASOS EL RESULTADO ES UN N´UMERO ENTERO POSITIVO.
1. En una feria artesanal en Cusco el precio de un tejido es proporcional a su área. Kimberly compó un tejido de 2 metros de largo y 1,5 metros de ancho a 80 soles y Hugo compró un tejido de la misma calidad que el de Kimberly, pero de 1,5 metros de largo y 1,2 metros de ancho. ¿Cuánto cost´o el tejido de Hugo?
2. Los números del 1 al 8 están escritos en ocho tarjetas de papel. Ana, Beatriz, Carla y Daniela eligen 2 tarjetas cada una de tal forma que las sumas de los dos números en sus tarjetas son iguales a 4, 7, 11 y 14, respectivamente. ¿Cuál es el mayor n´umero que eligió Carla?
3. Miguel tiene 60 caramelos y los distribuye en algunas bolsas de tal forma que no hay dos bolsas con la misma cantidad de caramelos y, además, ninguna bolsa queda vacía. ¿Cuántas bolsas como máximo tiene Miguel?
4. Martín tiene una hoja cuadrada de área 8 y la divide en siete piezas de Tangram, como se muestra en la siguiente figura:
Usando estas siete piezas él forma una nueva figura en forma de letra C:
Calcule el perímetro de esta nueva figura.
Observación: Las piezas de Tangram son 5 triángulos rectángulos isósceles, un paralelogramo y un cuadrado.
5. Decimos que un número natural es asombroso si es m´ultiplo de la suma de sus dígitos y también es múltiplo de la suma de los cuadrados de sus dígitos. Por ejemplo, 2023 es asombroso pues es múltiplo de 7 = 2+0+2+3 y también es múltiplo de 17 = 22+02+22+32. Encuentre el mayor número asombroso de cuatro dígitos que es múltiplo de 23.
6. Sea ABC un triángulo. Ubicamos un punto E sobre el segmento AC y punto D sobre el segmento BE de tal forma que BD = 8, BC = 9 y ∠ABC = ∠BCA = ∠CDE = ∠DEC.
Calcule la longitud de AB.
7. En algunas casillas del tablero de 10 × 10 mostrado se va a colocar una moneda, de tal manera que cada fila, cada columna y cada una de las dos diagonales del tablero contenga exactamente una moneda. Determine cu´antas monedas puede haber como m´aximo en las casillas sombreadas.
8. Determine el menor entero positivo n para el cual existen enteros positivos x1, x2, . . . , xn, no necesariamente distintos, tales que
9. Cuatro amigos van a una heladería que tiene helados de 3 sabores distintos. Cada uno pide cierta cantidad de helados (que puede ser 0) de tal manera que:
- Si alguien pide dos o más helados estos deben ser de sabores distintos.
- Ninguno de los sabores fue elegido por exactamente dos amigos.
- Cada sabor fue pedido por al menos un amigo.
Determine la cantidad de formas en las que pudieron realizar su pedido.
10. Sean a, b, c, d n´umeros reales tales que
Calcule el valor de 6(a + c)/(b + d)



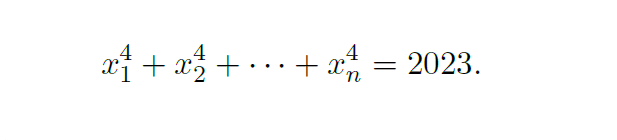

Publicar un comentario
Emplea un lenguaje de respeto a la comunidad al momento de dejar tu comentario. Recuerda que tu lenguaje te identifica como persona, el cambio de la educación empieza por ti.